`long`으로 표현되는 값을 `double`에 담아도 될까요?
처음 이 질문을 봤을 때, 직관적으로는 상관이 없을 듯해 보였습니다.
`long`은 8byte의 정수형을 담는 타입이고,
`double`은 같은 8byte 크기의 실수형을 담는 타입이며,
정수가 실수의 부분집합인 데다가 표현 범위도 `long`보다 `double`이 훨씬 크기 때문입니다.
근데 그런 뻔한 설명이 답이라면, 이 질문이 존재하지도 않았겠구나, 분명 어떤 문제가 있겠구나 하는 생각이 들었고, 이 질문에 대해 확실한 답을 하기 위해 알아본 내용을 글로 정리해보고자 합니다.
# 00. 자바의 정수형과 실수형
위에서 말씀드렸듯, `long`은 정수형을 담는 자료형이며, `double`은 실수형을 담는 자료형입니다.
둘의 차이를 비교하기 위해 먼저 자바의 정수형과 실수형에 대해 알아보겠습니다.
자바의 정수형
| 타입 | 범위 | bit | byte |
| byte | -128 ~ 127 (-2^7 ~ 2^7 - 1) | 8 | 1 |
| short | -32,768 ~ 32,767 (-2^15 ~ 2^15 - 1) | 16 | 2 |
| int | -21억 ~ 21억 (-2^31 ~ 2^31 - 1) | 32 | 4 |
| long | -922경 ~ 922경 (-2^63 ~ 2^63 - 1) | 64 | 8 |
정수형에는 `byte`, `short`, `int`, `long` 네 개의 자료형이 있습니다.
변수에 저장하려는 정수값의 범위를 고려하여 네 개의 정수형 중 하나를 선택하면 될 수 있겠으나...
JVM의 피연산자 스택이 피연산자를 4byte 단위로 저장하기 때문에 크기가 4byte보다 작은 `byte`나 `short`의 경우 값을 계산할 때 4byte로 변환하는 연산이 수행됩니다.
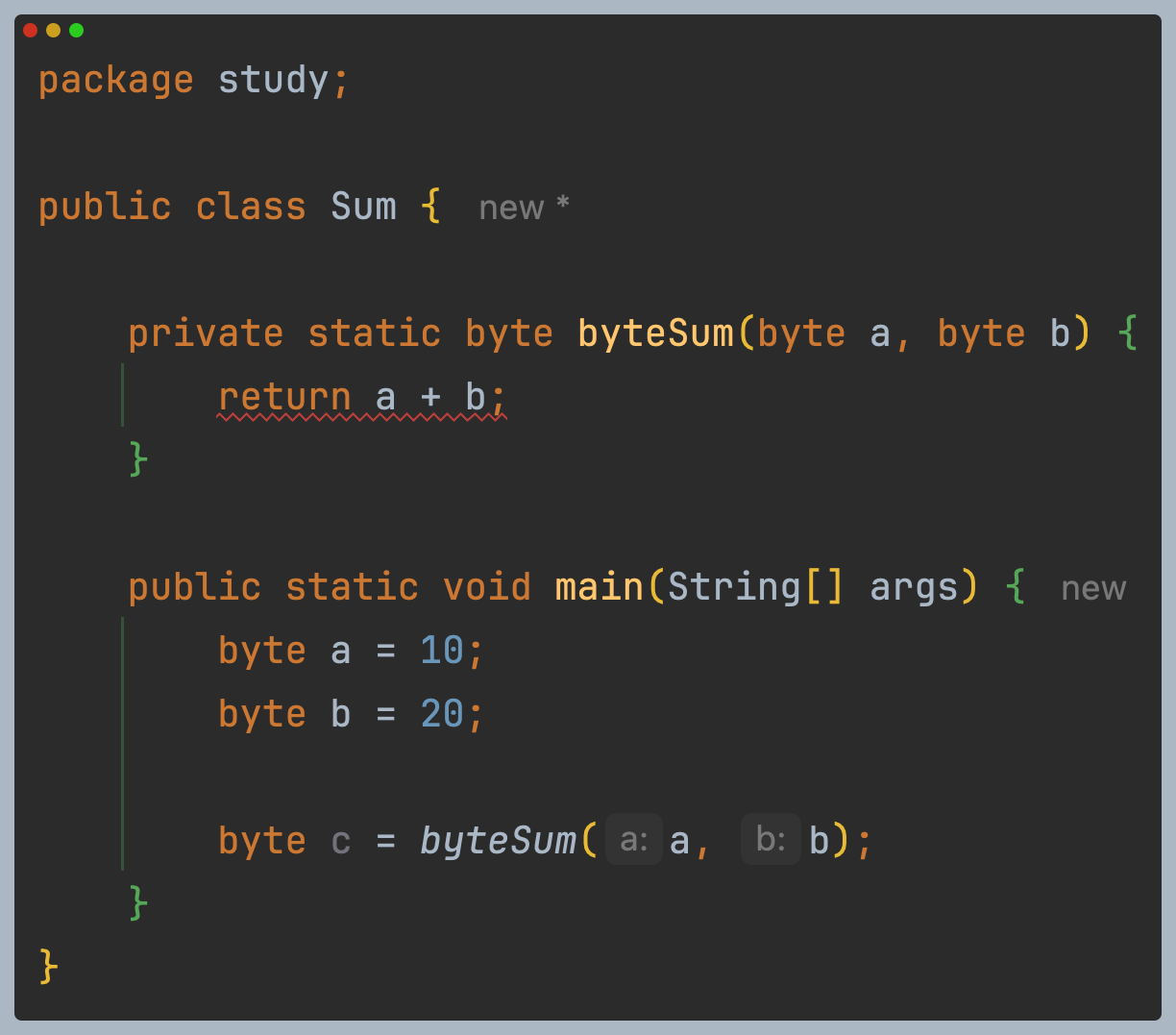
간단하게 테스트를 해보면 위와 같은 코드는 아래와 같은 컴파일 에러를 발생시킵니다.
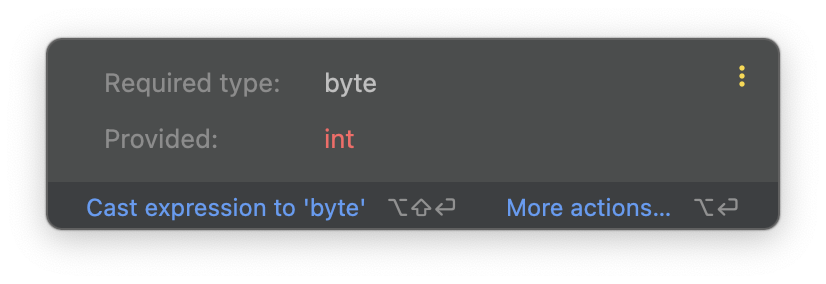
때문에 대부분의 경우에서 `int`나 `long`을 선택하는 것이 일반적입니다.
`byte`나 `short`를 고려하지 않아도 될 정도로 현대의 하드웨어 성능이 상향평준화 되기도 했고요.
자바의 실수형
| 타입 | 범위 | 정밀도 | bit | byte |
| float | 1.4 * 10^(-45) ~ 3.4 * 10^38 | 7자리 | 32 | 4 |
| double | 4.9 * 10^(-324) ~ 1.8 * 10^384 | 15-16자리 | 64 | 8 |
실수형에는 `float`, `double` 두 개의 자료형이 있습니다.
눈여겨볼 것이 정수형에는 없는 정밀도라는 개념이 실수형에는 있다는 것과,
같은 4byte, 8byte 자료형인 `int`나 `long`에 비해 `float`과 `double`의 표현 범위가 훨씬 크다는 것입니다.
이러한 이유들에 대해서는 이후 자세하게 풀어보겠습니다.
# 01. 자바에서 0.1은 0.1이 아니다
0.1 + 0.2는 0.3입니다.
실제로 자바 코드가 이 실수의 연산을 정확하게 수행하는지 코드로 확인해 보겠습니다.


결과가 기대하는 값 0.3이 아닌 0.30000000000000004000이 출력됨을 확인할 수 있습니다.
그 이유를 찾아보기 위해 이번에는 `BigDecimal` 클래스를 이용해서 0.1과 0.2를 내부적으로 어떻게 저장하는지 출력해서 확인해 보겠습니다.


`double` 0.1을 0.1이 아닌 0.1000000000000000055511151231257827021181583404541015625으로,
`double` 0.2를 0.2가 아닌 0.200000000000000011102230246251565404236316680908203125로 저장하고 있었습니다.
# 02. 부동소수점
위와 같은 결과가 발생하는 이유는 자바에서 정수형과 실수형 숫자를 저장하는 방식이 다르기 때문입니다.
정수형의 경우 비트 하나가 정확한 값 하나를 가집니다.
때문에 표현 범위 안에서는 값이 오차 없이 정확하게 표현됩니다.
숫자 10을 예로 들면,
10 = 1 × 2³ + 0 × 2² + 1 × 2¹ + 0 × 2⁰ 연산 결과에 따라
32비트를 사용하는 int 기준으로 00000000 00000000 00000000 00001010과 같이 저장합니다.
반면, 실수형의 경우 하나의 수가 비트를 나눠서 사용합니다.
32비트의 `float`을 예로 들면,
1비트는 부호 비트로,
8비트는 지수부로,
23비트는 가수부로 나누어 사용합니다.
`float` 10을 비트로 나타내면, 정규화 과정을 거쳐 아래와 같이 표현됩니다.
0 10000010 01000000000000000000000
(부호) (지수부) (가수부)
부동소수점의 구조를 좀 더 자세하게 알아보겠습니다.
위에서 말씀드렸듯 부동소수점에서는 주어진 비트를 아래와 같이 부호, 지수부, 가수부로 나누어 사용합니다.
[부호비트] [지수부] [가수부]
부호비트 + 지수부 + 가수부의 합은 `float`의 경우 32비트, `double`의 경우 64비트가 됩니다.
숫자 123000을 예로 들어 각 영역에 대해 이야기해 보겠습니다.
직관적인 위해 10진수 부동소수점으로 예로 들 것이며, 실제 자바에서는 IEEE-754를 따르는 2진수 부동소수점을 채택하여 사용합니다.
부호비트는 말 그대로 값이 양수인지, 음수인지 표현합니다.
양수의 경우 0, 음수의 경우 1로 표현합니다.
123000의 경우 양수이기 때문에 부호비트는 0을 가집니다.
가수부의 경우 숫자를 정밀하게 표현하는 부분입니다.
예를 들어 숫자 123000을 10진수 부동소수점으로 표현하면, 가수는 0이 반복되기 직전까지의 값인 1.23이 됩니다.
지수부의 경우 숫자의 크기(범위)를 표현합니다.
123000은 1.23 * 10⁵로 표현할 수 있습니다.
이때 5가 지수가 됩니다.
실제 자바에서는 정규화 전에 수를 2진수로 변환하는 과정이 있습니다.
10진수에서 123000을 1.23 * 10⁵로 표현했듯,
2진수에서는 정규화를 통해 1.xxxxx₂ × 2ⁿ 로 표현합니다.
최종적으로 정규화된 값을 각각 가수부와 지수부 비트 영역에 맞게 변환되어 저장됩니다.
위 코드에서 자바가 실수 0.1과 0.2를 값 그대로 저장하지 못하는 이유도 여기서 발생합니다.
0.1과 0.2는 2진수 변환 시 나누어 떨어지지 않는 무한소수로 변환됩니다.
자세한 건 아래에서 다루겠습니다.
이처럼 부동소수점은 정수형처럼 숫자 자체를 그대로 저장하는 방식이 아니라, 정규화된 가수와 지수를 이용한 하나의 표현식 형태로 숫자를 저장합니다.
여담이지만, 부동소수점에서 '부'는 아닐 부(不)가 아닌 뜰 부(浮) 자를 사용합니다.
분명 소수점이 고정되어 있지 않은 방식이라고 했는데 왜 '부동'이지? 라고 오해하는 경우가 있는데,
그게 아니라 소수점이 고정되어 있지 않고 떠다닌다고 이해하시면 될 것 같습니다.
영어로는 floating point라고 표현합니다.
# 03. 부동소수점과 정밀도
그럼 왜 굳이 자바에서는 실수형을 이와 같이 복잡한 과정을 통해 부동소수점으로 저장을 할까요?
현실 세계에 존재하는 수의 범위는 매우 넓습니다.
아주아주 큰 값도 있고,
아주아주 작은 값도 있으며,
소수점 아래로도 값이 길게 이어지는 경우가 있습니다.
컴퓨터는 이러한 다양한 수를 한정된 비트의 수로 다루어야 합니다.
만약 수 0.0000000000123을 값 그대로 저장하기 위해서는
반복되는 숫자 0을 여러 번 저장해야 하는 공간 낭비가 발생합니다.
하지만 (10진수 부동소수점이라 치고) 부동소수점으로 변환하여 저장한다면
가수 1.23과 지수 -11만 저장하면 됩니다.
덕분에 훨씬 넓은 범위의 값을 저장할 수 있으며,
같은 8byte, 16byte 정수형인 `int`나 `long`에 비해 `float`과 `double`의 표현범위가 더 넓은 이유가 이와 같습니다.
하지만, 부동소수점 방식에서는 가수부의 범위가 정해져 있습니다.
`float`의 경우 23비트를, `double`의 경우 52비트를 사용합니다.
만약 정규화된 가수가 지정된 가수부 비트범위를 초과하게 된다면, 뒤쪽 비트가 잘려나가고 가장 가까운 값으로 반올림되어 저장됩니다.
변환하고자 하는 값이 매우매우 크거나, 매우매우 작거나,
혹은 0.1, 0.2와 같이 2진수로 변환된 값이 무한 소수일 경우 값이 반올림되어 정확한 값 그대로를 저장할 수 없습니다.
이와 같은 이유로 자바의 실수형에는 정밀도라는 개념이 등장합니다.
가수부의 비트 수가 고정되어 있기 때문에, 표현할 수 있는 유효 숫자의 개수 또한 제한적입니다.
부동소수점에서 정밀도란 표현할 수 있는 숫자 전체 자릿수가 아니라, 오차 없이 정확하게 표현할 수 있는 유효 숫자의 개수를 의미합니다.
`float`의 경우 7자리, `double`의 경우 15~16자리의 10진수 정밀도를 가지며, 이 범위를 초과하는 자릿수는 반올림되어 저장됩니다.
`float`의 경우, 2진수 24자리(가수부 비트)가 10진수의 7-8자리와 같은 범위를 표현하기 때문에 7자리 까지는 값을 보장하게 됩니다.
이 때문에 숫자가 매우 커질수록 소수점 이하의 정밀도는 점점 줄어들게 됩니다.
# 04. long으로 표현되는 값을 double에 저장해도 될까?
지금까지 자바에서 실수형이 정확하지 않은 이유,
부동소수점과 정밀도에 대해 알아봤습니다.
그럼 다시 이 "`long`으로 표현되는 값을 `double`에 저장해도 될까?"라는 질문에 대한 대답을 생각해 보겠습니다.
`long`은 정수를 담는 자료형입니다.
모든 정수는 2의 거듭제곱의 합으로 표현할 수 있습니다.
그 말은 즉, 0.1이나 0.2와 같이 정수 범위를 벗어나는 실수가 2진수로 변환될 때 무한소수가 되는 케이스는 고려하지 않아도 된다는 의미입니다.
그렇다면 일단 일반적인 범위의 `long`값들은 `double`에 담아도 문제가 되지 않겠네요.
그다음으로 고려해야 할 것은 매우 큰 수입니다.
`double`의 정밀도는 15~16자리임을 위 표에서 확인했습니다.
`double`의 가수부는 52비트를 사용한다고 했습니다.
본 글에서는 다루지 않지만 `double`의 정밀도는 가수부 52비트에 히든 1비트를 포함하여 총 53비트입니다.
따라서 2진수로 연속된 정수를 정확하게 표현할 수 있는 범위는 -2⁵³ ~ 2⁵³ 입니다.
2⁵³은 9,007,199,254,740,992이며, 이 수는 16자리입니다.
때문에 double의 정밀도가 확실한 15자리나 16자리가 아닌 15~16자리가 나오는 것입니다.
즉, 절댓값이 2⁵³ 이하인 정수는 모두 `double`에서 정확하게 표현할 수 있습니다.
하지만 자바의 `long` 타입은 -2⁶³ ~ 2⁶³ - 1 까지의 수를 표현할 수 있습니다.
따라서, `long`이 표현할 수 있는 범위 중 일부 구간에서는, `long` 값을 `double`로 변환하는 과정에서 정확도의 문제가 생길 수 있습니다.
앞으로 저는 누군가 저에게 이 질문을 하면 아래와 같이 대답하겠습니다.
"자바에서는 실수형을 저장할 때 부동소수점 방식을 사용합니다. 부동소수점은 일정한 크기의 비트를 가수부와 지수부로 나누어 사용하는 방식입니다. 가수부는 값을 얼마나 정밀하게 표현할 수 있는지를 결정합니다. 만약 정규화된 가수의 길이가 가수부에 할당된 비트 수를 초과하게 되면, 초과하는 부분은 반올림으로 처리합니다. `double`의 가수부 정밀도는 53비트입니다. 따라서 절댓값이 2⁵³ 이하인 정수 값들에 대해서는 정확성을 보장하지만 2⁵³ 를 초과하면 값이 변질될 수 있습니다. `long`은 절댓값 2⁵³ 이상의 값을 표현할 수 있습니다. 따라서, 정수형 -> 실수형 변환이라 해서 무턱대고 `long`을 `double`로 변환했다가는 일부 구간에서 값이 변질될 수 있습니다."
# 05. 매우 큰 값을 정확하게 표현하고 싶다면?
정수형은 값을 정확하게 저장하지만 표현 범위가 제한적이고
실수형은 매우 큰 값을 저장할 수 있지만, 저장한 값이 정확하지 않을 수 있습니다.
그러면, 매우 큰 값을 정확하게 표현하고 싶다면 어떻게 해야 할까요
`java.math` 패키지의 `BigDecimal` 클래스를 이용하는 것으로 해결할 수 있습니다.
`BigDecimal`은 숫자를 10진수 형태로 관리하여 부동소수점 방식의 오차를 완전히 해결하는 클래스입니다.
`BigDecimal`은 숫자를 소수가 아닌 정수와 소수점 위치로 나누어 저장합니다.
0.123을 저장할 때 123이라는 정수(`BigInteger`)와 3이라는 소수점 위치를 따로 보관합니다.
때문에 숫자를 2진수로 변환해서 억지로 끼워 맞추다가 0.1, 0.2와 같은 무한소수 문제도 발생하지 않으며,
정수부를 내부적으로 `int []` 배열에 저장하기 때문에 이론상의 표현 범위도 무한입니다. (물리적으로는 21억 자리)
물론, 단점도 있습니다.
`double`이나 `long`의 경우 고정 크기의 메모리 공간에 값만 딱 들어있어, 스택 영역에서 매우 빠르게 액세스 되지만,
`BigDecimal`은 객체입니다.
숫자 값을 저장하기 위해 내부적으로 `BigInteger` 객체를 또 가지고 있으며, `BigInteger`는 다시 숫자를 `int []` 배열에 저장합니다.
즉, 값을 하나 계산할 때마다 힙 메모리에 새로운 객체를 생성하고 할당해야 합니다.
성능과 정확도 사이의 트레이드오프를 계산하여 primitive 자료형을 사용할지, `BigDecimal`을 사용할지 결정하시면 되겠습니다.
화이팅
📚 References
'Java' 카테고리의 다른 글
| JVM 메모리 구조와 동작 과정 파헤쳐보기! (0) | 2025.06.04 |
|---|---|
| Java Stream API 이해부터 '잘' 사용하는 방법까지 (1) | 2025.04.11 |