URL Shortner 웹사이트 제작 중에 있습니다.
프로젝트의 목적은 다음과 같습니다.
첫 번째로는 스터디의 취지에 따라 초당 쓰기 요청 1,000건과 초당 읽기 연산 10,000건의 트래픽을 10년간 안정적으로 감당하는 대규모 시스템을 직접 설계하고 구현하는 것이고요.
두 번째는 URL Shortner라는 도메인에 대한 경험과 인사이트를 얻어가는 것이었습니다.
이 중 저는 도메인 로직을 설계하면서 고민하고 공부하면서 얻은 부분들 중 글로 남기면 좋을 만한 내용이 있어서 관련해서 적어보게 되었습니다.
대규모 시스템 설계에 대한 내용도 쓸 이야기들이 있는데.... 시간이 되면 다음에 꼭 작성하기로.....
소스코드는 깃허브 레포지토리에서 확인하실 수 있습니다.
https://github.com/LeeEuyJoon/lilling-be
# 00. 변환값의 자릿수
URL Shortner는 간단하게 긴 url을 보기 좋게 짧은 URL로 재생성하여 짧은 URL로 들어온 요청을 원본 주소로 리다이렉트 시켜주는 프로그램입니다.
이 서비스에서의 핵심 도메인 로직은 당연 원본 URL을 짧은 URL로 재생성하는 과정이라고 볼 수 있습니다.
이를 테면, https://luti-dev.tistory.com/18 이런 URL을 lill.ing/xX59NVu 이렇게 짧은 URL로 바꿔주는 방식이죠.
그리고 사실상 저 짧은 URL중 도메인 네임 이후 들어오는 패스 파라미터 ("3JBT6AU") 부분에 해당하는 문자열 값을 어떻게 생성하느냐가 관건입니다.
앞서 말씀드렸듯, 초당 쓰기 요청 1,000건에 대해 10년 운영 가능한 시스템을 설계하는 것이 목적입니다.
초당 쓰기 요청 1,000건이면 하루에 대략 1억개의 url을 생성해야 하고요
10년이면, 1억 * 365 * 10 = 3650억 개의 고유하면서도 길이가 짧은 값을 확보하는 로직이 필요합니다.
변환 값에 대해 각 자리마다 숫자와 알파벳 대소문자가 들어갈 수 있다고 한다면, 총 62종류의 문자가 들어갈 수 있습니다. (0-9, a-z, A-Z)
3650억 개의 고유한 변환값을 확보하기 위한 최소 자릿수를 계산해 보면
class FindN {
public int solution(int digit, long estimation) {
long value = digit;
int exponent = 1;
while (value < estimation) {
value *= digit;
exponent++;
}
return exponent;
}
}@Test
void test1() {
FindN findN = new FindN();
int digit = 62;
long estimation = 365_000_000_000L;
System.out.println("결과: " + findN.solution(digit, estimation));
}
결과가 7이 나옵니다.
62의 7승이 약 3조 5천억이기 때문에 7 자리면 프로젝트의 계략적 추정치인 3650억 개의 변환값을 확보하고도 한참 남습니다.
사실 이 값은 10년이 아니라 111년까지도 커버가 되는 자릿수입니다.
# 01. 변환 로직
## 해쉬 함수
자릿수는 정해졌고요, 변환 로직에 대해 생각해봐야 하는데...
가장 먼저 떠오르는 방식은 해시 함수가 있습니다.
해시 함수는 임의의 길이의 데이터를 고정된 길이의 값으로 변환하는 수학적 알고리즘입니다.
같은 입력에 대해서는 항상 같은 해시값을 생성하고, 입력값이 조금만 달라져도 전혀 다른 해시값이 나옵니다.
(다른 얘기이긴 한데, 한 세 달 전쯤 정말 합격하고 싶었던 회사의 면접에서 URL Shortner에 대한 시스템 설계를 테스트했고요, 그때의 저는 URL 변환 로직에서 해쉬 함수를 사용하겠다고 대답했습니다.)
하지만 이 해쉬 함수를 변환 로직에 사용하기에는 제한적인 부분들이 있습니다.
먼저, 해쉬 함수는 기본적으로 해싱 결과의 길이가 긴 편입니다.
수십 자리를 넘어가는 경우도 있는데, 이 수십 자리 값을 그대로 shortned url로 사용하기에는... 원본 url이 더 긴 경우도 허다하지 않을까 싶고요.
그렇다고 슬라이싱 해서 앞에 몇 자리만 사용하기에는 충돌을 피할 수가 없을 것입니다.
URL Shortner에서는 같은 단축 url이 두 번 나오면 치명적인 충돌이 되기에 해시 충돌 자체를 원천적으로 방지해야 합니다.
## Base-62
그래서 더 좋은 방법은 Base-62 진법 변환이라고 생각했습니다.
62진법은 수를 표현하기 위해 총 62개의 문자열을 사용하는 진법이고, 이 결과를 변환값으로 사용하는 것입니다.
일단 여러 진법 변환 방식들 중 Base-62를 사용하는 이유는 변환값 각 자리에 들어갈 수 있는 문자가 딱 62개이기 때문입니다.
그럼 이제 62진법 변환을 위한 키가 필요하겠습니다.
진법 변환이라는 것이 입력값에 대해 1대 1로 고유한 문자열로 표현되는 것이며, 앞서 계략적 추정치 커버를 위한 최대 자릿수를 7자로 정했기 때문에, 키는 3조 5천억 이하의 고유한 정수가 필요합니다.
# 02. Id 스크램블링 여정
## 순차 Id
우선 처음에는 1, 2, 3... 이렇게 순차적으로 증가하는 값을 사용하고자 했습니다.
가장 간단하고 에러케이스가 발생하지 않는 접근이라고 생각했습니다.
문제는 순차적으로 1씩 증가하는 값은 변환값도 62진법 세계에서 1씩 증가한다는 것이었습니다.
표로 확인해 보면
| 10진수 ID | 62진 표현 | 단축 url |
| 1 | 1 | https://lill.ing/1 |
| 2 | 2 | https://lill.ing/2 |
| 3 | 3 | https://lill.ing/3 |
| 36 | a | https://lill.ing/a |
| 37 | b | https://lill.ing/b |
| 38 | c | https://lill.ing/1c |
위와 같습니다.
단축 url의 결과가 대놓고 패턴이 보인다는 점에서 보안상의 문제도 우려가 되고 사이트의 신뢰도 보장하기가 어려워 보입니다.
사실 키를 따로 키 발급 서버에서 관리하고 각 app 서버에 서로 다른 고유한 키를 뿌리는 형태로 시스템을 구축했기 때문에 위와 같이 극단적으로 패턴이 읽히지는 않겠지만, 그대로 두는 것은 바람직하지 않아 보입니다.
## 선형식 기반
그래서 이 순차 키값을 스크램블링 하는 로직이 무조건 필요하겠다 싶었습니다.
문제는 정말 무작위적으로 스크램블링만 해서는 안되고 고유성을 철저하게 보장해야 한다는 것이었습니다.
스크램블 하다가 기존에 존재하는 키와 같은 키가 생성되어 버리면 두 개의 원본 url이 하나의 단축 url을 사용하게 되는 시스템 장애가 발생하게 되기 때문입니다.
여기서 저는 선형식과 모듈러 연산을 통해 접근을 해봤습니다.
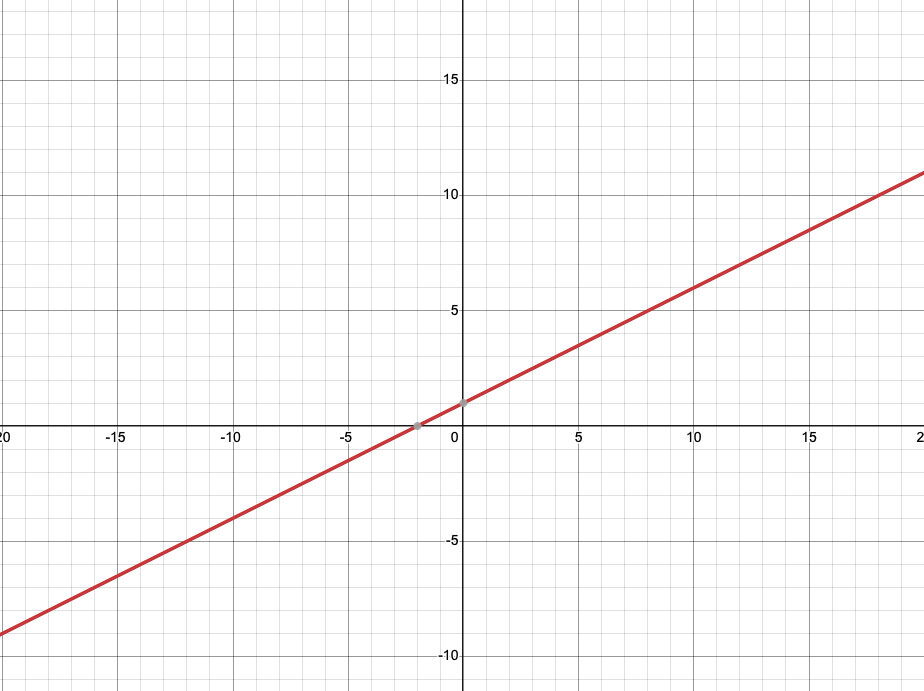
아이디어는 이렇습니다.
1차 함수 그래프는 증가함수입니다.
이 말은 서로 다른 x값에 대해 무조건 고유한 y값을 1대 1로 가지고 있다는 뜻입니다.
그렇다면 입력하는 순차 키값에 대해 서로 다른 스크램블 아이디를 확보할 수 있을 것이라 생각했습니다.
수식으로 표현하면 다음과 같습니다.
$$
Encoded_ID = (A * id + B) mod M
$$
A와 B는 임의의 상수이며 M은 생성하고자 하는 값의 최댓값입니다.
즉, 기존 ID를 M으로 나눈 나머지를 취함으로써 항상 값을 0 이상 M 미만으로 제한할 수 있고, 결과적으로 특정 범위 내에서 ID가 벗어나지 않도록 보장합니다.
이때 A와 M은 서로수여야만 한다는 조건이 붙습니다.
만약 A와 M이 공약수를 가진다면, 그 공약수에 의해 일부 숫자는 절대 나오지 않게 됩니다.
예를 들어 A = 4, M = 8이라면 결과는 0, 4, 0, 4, 0, 4,...처럼 일부 값만 반복됩니다.
A와 M이 서로수 관계여야만 이 수식이 M 전체를 완전히 순회하며 모든 ID가 1:1로 대응되는 완전한 순열을 만듭니다.
이 로직으로 구현을 해보고 테스틀 해보았는데요,
먼저 A를 17, B를 35로 두고 테스트해봤습니다.
| 10진수 ID | 선형식 결과 (17 x id + 35) mod M | 62진 표현 | 단축 url |
| 1 | 52 | q | https://lill.ing/q |
| 2 | 69 | 17 | https://lill.ing/17 |
| 3 | 86 | 10 | https://lill.ing/1O |
| 36 | 647 | AR | https://lill.ing/AR |
| 37 | 664 | Ai | https://lill.ing/Ai |
| 38 | 681 | Az | https://lill.ing/Az |
음... 순차 값을 바로 진법 변환 할 때에 비해서는 패턴이 직관적으로 보이지는 않지만
대충 비슷한 자릿수와 비슷한 앞부분이라는 패턴이 보입니다.
혹시나 A와 B값이 작아서 그런가 싶어 더 큰 값을 넣어서 테스트해 봤습니다.
이번에는 값을 A=56,800,235,583, B=916,132,831 이렇게 넣어봤고요, 결과는
| 10진수 ID | 선형식 결과 (17 x id + 35) mod M | 62진 표현 | 단축 url |
| 1 | 57,716,368,414 | 10zzzzy | https://lill.ing/10zzzzy |
| 2 | 114,516,603,997 | 20zzzzx | https://lill.ing/20zzzzx |
| 3 | 171,316,839,580 | 30zzzzw | https://lill.ing/30zzzzw |
| 36 | 2,045,724,613,819 | a0zzzzP | https://lill.ing/a0zzzzP |
| 37 | 2,102,524,849,402 | b0zzzzO | https://lill.ing/b0zzzzO |
| 38 | 2,159,325,084,985 | c0zzzzN | https://lill.ing/c0zzzzN |
위와 같습니다.
여기서도 보이듯이, 큰 A와 B 값을 사용해도 선형식 특유의 패턴이 보입니다.
앞에 숫자/문자가 하나씩만 바뀌고 0zzzz가 고정된 값이 남습니다.
이러한 패턴이 드러나는 이유를 생각해 보면....
선형식은 모든 구간에서 기울기가 일정하다는 점에서 근본적인 한계를 가집니다.
즉, 입력값이 일정하게 증가하면 출력값도 일정한 간격으로 증가한다는 점입니다.
결과적으로 값이 커지더라도 규칙적인 패턴이 그대로 유지됩니다.
## 지수함수 기반
그다음 접근은 지수함수였습니다.
기존 선형식의 문제점이 모든 구간에서 기울기가 일정하다는 것이었다면,
증가함수이면서 모든 구간에서 기울기가 다른 지수함수를 이용하면 눈에 보이는 패턴 없이 값이 잘 스크램블 되지 않을까 하는 아이디어였습니다.

문제는... 지수함수의 출력값이 너무 빠르게 커져버린다는 것이었습니다.
입력값이 최대 3조 5천억까지 들어가야 하는데 , 모든 구간에서 기울기가 증가하여 점점 무한에 가까워지기 때문에 택도 없을 거라 판단하여 다른 방법을 찾기로 했습니다.
## XORShift
그다음 접근은 XORShift 연산입니다.
XOR은 비트 연산에서 자릿수를 비교하여 서로 값이 다르면 1, 같으면 0으로 치는 연산입니다.
예를 들어,
0101
0011
----
0111 → 10진수로 7
이러한 연산입니다.
여기서 포인트는 XOR은 자기 자신과 XOR 하면 0이 되고, 0과 XOR 하면 자기 자신이 남아 가역적인 성질을 가지고 있습니다.
그리고 비트 시프트 연산은 비트를 오른쪽이나 왼쪽으로 미는 연산입니다.
예를 들어,
x = 0001 0110 (10진수 22)
를 x << 1 (왼쪽으로 한 칸 이동) 한다면
0010 1100 (10진수 44)
이렇게 되는 거죠.
이때 밀고 나서 반대쪽에서 추가된 자릿수들은 모두 0으로 둡니다.
XORShift는 이 두 동작을 같이 쓰는 연산입니다.
x ^= (x << 13);
x ^= (x >>> 7);
x ^= (x << 17);
위 코드의 의미는 값 x를 여러 방향으로 비트 단위 시프트하면서 그 결과를 다시 x 자신과 XOR 하는 과정을 세 번 반복한다는 뜻입니다.
이때 왼쪽으로 밀 때는 부호 개입이 없어 << 연산으로 그냥 사용하고,
오른쪽으로 밀 때는 부호비트가 들어오면 섞임이 깨지기 때문에 무조건 0으로 채우는 >>>를 써서 부호를 배제합니다.
사실 여기서도 왼쪽이나 오른쪽으로 밀 때 아무 값이나 사용하면 안 되는데,
XORShift의 전체 변환은 2진수 유한체 위에서 정의된 선형 변환입니다.
이때 Shift 연산과 XOR 연산을 결합한 형태의 행렬식이 0이 아니면, 즉 역행렬이 존재하면 가역적이라고 말할 수 있으며,
가역적이라는 것은 곧 값의 변환 전 후의 값이 1대 1로 매핑되어 있다 -> 변환값의 고유성을 보장한다는 의미로 이어집니다.
이걸 또다시 말하면, 무조건 full-rank가 되는 시프트 조합으로 적용해야 최종적으로 변환된 값을 키로 사용할 수 있다는 말이구요.
그 조합은 감사하게도 2003년에 Marsaglia가 81개의 조합을 찾아내어 정리해 놨습니다.
그래서 가역성을 보장하는 시프트 조합 중 하나를 선택하여 로직에 적용하고 62진법 변환하고 테스트한 결과

짠
드디어 패턴이 전혀 보이지 않는
완전 무작위적인 7자리 이하의 변환값을 확보할 수 있었습니다.
# Feistel Cipher
(이후 추가된 글입니다.)
## XORShift 연산의 문제점
XORShift 연산을 통해 아주 무작위적인 변환값을 확보할 수 있었습니다.
문제는 ....
XORShift는 64비트 공간 (약 1800경)에서의 고유성을 보장하는 연산이기 때문에 결과적으로 3조 5천억 이하의 고유한 순차값들을 입력한다 한들 그 결과가 3조 5천억 이하를 보장하지 않고 64비트 전체 공간에서 랜덤 하게 나온다는 것이었습니다....!
그래서 저는 이걸 선형식에서 모듈러를 쳤듯이 결과를 M값 (3조 5천억)으로 나눈 나머지를 사용하겠다는 아이디어로 위 스크린샷 처럼 랜덤한 변환값을 뽑아낸 것이었는데....
그것은 약 1800경의 범위의 숫자들을 3조 5천억 안으로 밀어 넣는 것이라 이론상 숫자가 점점 채워질수록 충돌이 날 확률이 점점 더 커지는 상황이었습니다.
4, 7, 10 이 숫자들을 다 3으로 나누면 나머지가 모두 1이 되는 것처럼 말이죠.
## Feistel Cipher
그래서 그다음으로 접근했던 방법은 Feistel Cipher입니다.
Feistel Cipher는 대칭키 블록 암호의 기본 설계 원리로 사용되는 암호화 구조 혹은 설계 방식입니다.
구조를 살펴보겠습니다.

먼저 입력값을 두 부분으로 나눕니다. -> L0, R0
한 공간의 범위를 정할 때는 보통 공간 크기가 M이라면 이를 ceil(√M)으로 계산하여 m으로 사용합니다.
F는 무작위성을 부여하는 함수입니다.
이 L0과 R0을 아래와 같은 방식으로 업데이트합니다.
R1 = (L0 + F(R0)) mod m
L1 = R0이러한 형태의 업데이트를 한 라운드라고 표현하며, 몇 차례에 걸쳐 진행합니다.
고전적인 방법은 R을 업데이트할 때 XOR 연산을 수행하는 것입니다.
다만, 저의 경우 정수 범위에서 명확한 도메인 제어가 필요했기 때문에 덧셈과 모듈러 연산을 결합하여 사용했습니다.
이는 항상 결괏값이 0 이상 M의 제곱근(m) 미만임을 보장합니다.
XOR 연산을 사용할 경우 값의 범위를 보장하기가 힘들어집니다. (앞서 스크램블링 알고리즘을 XORShift로 구현했다가 문제가 발생한 이유와 유사하죠.)
## Feistel Cipher가 고유성을 보장하는 이유?
고유성을 보장한다는 말은 가역적이다라는 말로 다르게 표현할 수 있습니다.
하나의 입력에 대한 결과가 단 하나라면, 결과를 통해 원래의 입력값을 다시 알아낼 수 있겠죠.
Feistel Cipher에서 고전적으로 각 라운드에 사용하던 XOR 연산이라던가, 제가 사용한 덧셈 연산은 모두 역연산이 존재합니다.
(XOR 역연산은 XOR 한번 더하기, 덧셈의 역연산은 빼기)
라운드를 여러 번 반복해도 각 라운드가 가역 함수의 조합이므로 전체 네트워크 역시 완전한 가역성을 유지합니다.
따라서 항상 입력과 출력이 1:1로 대응되도록 보장합니다.
## Cycle Walking
L과 R의 크기를 ceil(√M)로 계산하여 사용한 이유는 전체 공간이 m * m >= M 이 되도록 보장하기 위함입니다.
즉 , Feistel Cipher가 표현할 수 있는 전체 공간은 M 보다 약간 넓은 m *m이고 해당 로직에서 실제로 사용하고 싶은 ID의 범위는 0 <= id < M 입니다.
따라서 결괏값이 M 이상을 벗어날 경우, 그 값을 다시 입력으로 넣어 Feistel 연산을 한 번 더 수행하여 값이 0 <= id < M 구간으로 들어오도록 반복하며, 이 과정을 Cycle Walking이라고 합니다.
Cycle Walking은 Feistel Cipher의 기본 구조에 속한 요소는 아니지만 출력 도메인을 제한된 범위로 강제할 때 자주 함께 사용되는 보완 기법입니다.
## 테스트 (속성 기반, full-range, 가역성 검증)
지금까지는 일단 Feiestel Cipher를 이용한 변환 방식이 수학적으로 가역적이고, 충분히 비선형적인 무작위성을 제공하며, 고유하며 범위를 지키는 출력을 보장한다고 생각하지만, 혹여나 또 한 번 이 알고리즘의 하자가 발견될 수 있기에 철저하게 테스트를 진행하기로 했습니다.
먼저 입력값 분기를 지정하여 기본 동작을 테스트하는 단위 테스트는 넘어가겠습니다.
속성 기반 테스트 (jqwik)
변환값의 고유성을 테스트하기 위해서는 먼저 수많은 랜덤 한 값에 대한 반환이 모두 고유하며 M 미만인지 테스트해야 한다고 생각했습니다.
이와 같은 이유로 JUnit을 활용한 예시 기반 테스트가 아닌 jqwik를 사용하여 속성 기반 테스트를 진행하였습니다.
public class PropertyBasedTest {
private static final long M = 3_521_614_606_208L;
// 리스트 크기를 파라미터로 받아서 Arbitrary 생성
Arbitrary<List<Long>> idListOfSize(int size) {
return Arbitraries.longs()
.between(1, M - 1) // 1 이상 M-1 이하의 랜덤한 값을
.list() // 리스트로
.ofSize(size) // size 크기만큼
.uniqueElements(); // 고유한 값으로 생성
}
@Group
class ScramblePropertyTests {
// 프로바이더 정의
@Provide Arbitrary<List<Long>> ids_hundred() { return idListOfSize(100); } // ID 100개
@Provide Arbitrary<List<Long>> ids_10_thousand() { return idListOfSize(10_000); } // ID 1만개
// @Provide Arbitrary<List<Long>> ids_million() { return idListOfSize(1_000_000); } // ID 100만개 -> 안돌아간다...
@Property(tries = 10000)
@Label("Feistel Cipher 고유성 테스트 - 100개 ID 10000번")
void testScrambleWith100Ids(@ForAll("ids_hundred") List<Long> ids) {
runScrambleTest(ids);
}
@Property(tries = 100)
@Label("Feistel Cipher 고유성 테스트 - 1만개 ID 100번")
void testScrambleWith10000Ids(@ForAll("ids_10_thousand") List<Long> ids) {
runScrambleTest(ids);
}
// @Property(tries = 1)
// @Label("Feistel Cipher 고유성 테스트 - 100만개 ID 1번")
// void testScrambleWith1MillionIds(@ForAll("ids_million") List<Long> ids) {
// runScrambleTest(ids);
// }
}
// 공통 테스트 로직 메서드
void runScrambleTest(List<Long> ids) {
IdScrambler scrambler = new IdScrambler(M, 13, 7, 17);
HashSet<Long> seen = new HashSet<>();
for (Long id : ids) {
Long scrambled = scrambler.scramble(id);
assertThat(scrambled)
.isGreaterThanOrEqualTo(0L)
.isLessThan(M);
assertThat(seen).doesNotContain(scrambled);
seen.add(scrambled);
}
}
고유성을 체크하기 위해 각 테스트에서 HashSet을 생성하여 값을 담을 때마다 중복 체크를 하구요.
총 100개의 입력 id를 변환하고 검증을 10,000번,
그리고 총 10,000개의 입력 id를 변환하고 검증을 100번 수행했습니다.
문제는 100만 개의 id부터는 메모리가 견디지 못하고 테스트가 정상적으로 동작하지 않는다는 것인데...
총 범위 3조 5천억 중 고작 100만 개의 고유성도 체크하지 못하면 아직 로직에 대한 신뢰가 부족하다고 생각했습니다.
Full-Range Test
그러하여 이번에는 전체 범위 M 값을 실제 서비스 로직이 3조 5천억 대신 100만의 숫자를 넣어 고유한 1~100만의 id로 고유한 100만 개의 랜 id를 반환하는지 테스트하고자 했습니다.
이 테스트는 주어진 M 값에 꽉 차는 양의 id가 주어졌을 때 정말 M개의 고유한 id를 생성하는지 검증입니다.
(속성 기반 테스트에서는 사전에 LIst에 객체 타입인 Long 객체를 100만 개 생성하는 동작이라 메모리 부담이 있었고, full range 테스트에서는 원시타입 long 형을 사용할 수 있는 상황이라 메모리 부담 없이 테스트를 성공할 수 있었습니다.)
```
public class FullRangeTest {
@Test
@DisplayName("Feistel Cipher 고유성 증명 - M=1,000,000 전체 범위 테스트")
void fullRangeTest() {
long smallM = 1_000_000L; // 100만
IdScrambler scrambler = new IdScrambler(smallM, 13, 7, 17);
HashSet<Long> set = new HashSet<>((int) smallM);
for (long id = 0; id < smallM; id++) {
// 알고리즘 적용
Long scrambled = scrambler.scramble(id);
// 출력 범위 검증
assertThat(scrambled)
.as("ID: %d, 스크램블된 값이 범위를 벗어났습니다: %d", id, scrambled)
.isGreaterThanOrEqualTo(0L)
.isLessThan(smallM);
// 고유성 검증
if (!set.add(scrambled)) {
fail("중복된 스크램블된 ID가 발견되었습니다. ID: " + id + ", 스크램블된 값: " + scrambled);
}
}
// 5. 최종 검증: 루프가 끝난 후, 100만 개의 고유한 ID가 나왔는지 확인
assertThat(set.size())
.as("스크램블된 ID의 개수가 일치하지 않습니다.")
.isEqualTo(smallM);
}
}
가역성 검증 테스트
앞서 말씀드렸듯이 결괏값이 고유하다는 가역적라는 표현으로 바꿔 말할 수 있습니다.
스크램블링 알고리즘을 통해 얻은 값을 다시 역변환하여 원본 값을 찾아낼 수 있다면 그 알고리즘은 가역성을 보장한다고 말할 수 있습니다.
이 가역성을 검증하기 위해 따로 Feistel Cipher를 역연산 하는 메서드를 만들어 unscramble 테스트를 진행했습니다.
public class ReversibilityTest {
private static final long M = 3_521_614_606_208L;
private final IdScrambler scrambler = new IdScrambler(M, 13, 7, 17);
@Property()
@Label("Feistel Cipher 가역성 테스트 - ID 복원 검증")
void testReversibility(
@ForAll @LongRange(min = 0, max = M - 1) long originalId
) {
// 알고리즘 실행
Long scrambled = scrambler.scramble(originalId);
Long unscrambled = scrambler.unscramble(scrambled);
// 가역성 검증
assertThat(unscrambled)
.as("원본 ID: %d, 스크램블된 값: %d, 복원된 값: %d",
originalId, scrambled, unscrambled)
.isEqualTo(originalId);
}
}
테스트 결과

속성 기반 테스트, full-range 테스트, 가역성 검증 테스트를 모두 통과했습니다.
이로써
입력값 0 ~ 3조 5천억에 대해
아주 무작위적이고
고유하며
출력 또한 0 ~ 3조 5천억의 범위를 지키는
변환 체계를 구축했으며,
결과적으로 고유하고 무작위적인 7자리 변환값을 만들어 short url을 생성할 수 있게 되었습니다.
최종 변환 파이프라인은 아래와 같습니다.
1. KGS로부터 순차 ID 발급
2. Feistel Cipher Scrambling (Additive + XORShift + Cycle-Walking)
3. Base62 인코딩
4. Short URL 반환
base 62 인코딩을 위한
순차적 id -> 선형식 기반 스크램블링 -> XORShift 스크램블링 -> Feistel Cipher까지
며칠이나 저를 힘들게 했던 인코딩 여정이 드디어 끝났습니다
너무 지엽적인 도메인 로직에 시간을 너무 많이 쓴 건 아닌가 싶지만....
언젠가 도움이 되기를...
하 이걸 해보고 그때 면접에 들어갔더라면....!