과제랑 프로젝트랑 시험 준비까지 하면서 조금 바쁘네요...
그래서 이번 주는 기말고사 범위에 있는 Transformer 아키텍처에 대해 정리하는 것으로 날먹 한 번 하겠습니다.
Transformer는 사실 오늘 작성할 포스트의 챕터 하나하나만 따로 별도의 글로 작성해야 할 정도로 깊고 넓은 분야의 LLM 모델입니다.
그런데 이번 포스트에서는 트랜스포머의 자세한 부분까지 구체적으로 뜯어 파헤치기보다는 시험에 나올 정도로만 전반적인 흐름과 구성요소를 살펴보는 느낌으로 알아보겠습니다.
# 00. Transformer?
대 AI의 시대에서 현시대를 이끌어가는 대부분의 LLM들은 Transformer 아키텍처를 기반으로 설계되었습니다.
저희가 흔히 자주 사용하는 Open AI의 GPT부터 구글의 Gemini, Anthropic의 Claude, Meta의 LLaMA, DeepSeek까지도 모두 Transformer 아키텍처를 기반으로 하며, 사실 Transformer 기반이 아닌 LLM 모델을 찾기가 더 힘든 지경입니다.
트랜스포머의 등장은 그리 오래되지는 않았습니다.
2017년 『Attention Is All You Need』 논문을 구글에서 발표함으로써 세상에 처음 공개가 되었고, 기존 RNN에 비해 성능뿐만 아니라 모델 학습 속도까지도 큰 폭으로 앞섰기 때문에 LLM이 크게 발전하게 되는 근간이 되었다고 볼 수 있습니다.
기존 RNN 기반 모델의 한계
트랜스포머의 등장 이전에는 RNN(Recurrent Neural Network) 기반의 언어 모델들이 주를 이루었습니다.
RNN은 입력 시퀀스의 시간적 순서를 모델링하기 위해 고안된 신경망입니다.
과거 시점의 정보를 은닉 상태에 저장해 두고, 이를 기반으로 다음 출력을 예측합니다.
쉽게 풀어서 사람이 글을 읽는 것과 같이 텍스트를 순차적으로 입력한다고 볼 수 있습니다.

이러한 RNN의 순차적 처리라는 특징 때문에 분명한 한계가 존재했습니다.
LSTM(Long Short-Term Memory)과 같은 기법을 통해 극복하고자 하는 시도가 있었지만, 결국 long-term dependency (장기적 의존성 학습) 문제를 근본적으로 해결하기에는 구조적으로 취약했습니다.
층을 깊이 쌓으면 Vanishing Gradient나 Exploding Gradient 문제가 발생하는 경우가 있었습니다.
다시 말하면, 입력이 길어질수록 먼저 입력한 토큰의 정보가 희석되거나, 반대로 역전파 시 계산된 기울기가 너무 크게 발산해 가중치가 한 번에 매우 크게 갱신되는 문제가 있었다고 볼 수 있었습니다.
또한 병렬 처리가 불가능했기 때문에 학습 속도가 느리다는 점도 큰 문제로 남아있었습니다.
이러한 문제점들을 Transformer가 어떻게 극복하고 LLM 아키텍처의 표준이 되었는지 해당 포스트에서 설명하도록 하겠습니다.
Transformer 구성 요소
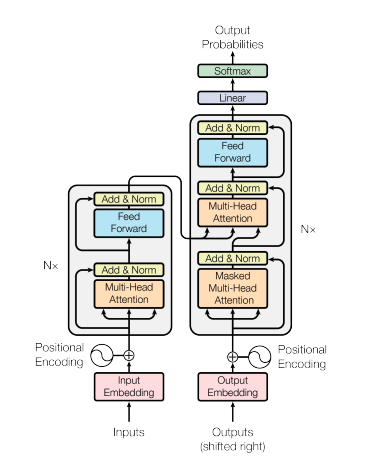
Transformer의 구성을 개략적으로 살펴보겠습니다.
먼저, Transformer는 크게 Encoder와 Decoder로 이루어져 있습니다.
그림의 왼쪽 상자가 언어를 '이해'하는 역할을 하는 Encoder이고요,
그림의 오른쪽 상자는 언어를 '생성'하는 역할의 Decoder입니다.
입력부터의 출력까지의 흐름을 보자면
먼저 공통적으로 입력을 Embedding 층을 통해 임베딩으로 변환하고 Positional Encoding(위치 인코딩) 층에서 문장의 위치 정보를 더합니다.
Encoder에서는 Layer Normalization(층 정규화), Multi-head attention(멀티 헤드 어텐션), Feed forward 층을 거쳐 문장을 이해하고 그 결과를 Decoder로 전달합니다.
Decoder에서는 Encoder에서와 유사하게 Layer Normalization, Multi-head attention 연산을 수행하면서 Cross attention 연산을 통해 인코더가 전달한 데이터를 출력과 함께 종합하여 Feed forward 층을 거쳐 결과를 생성한다고 볼 수 있습니다.
# 01. Perceptron과 MLP
Transformer의 각 계층에 대해 알아보기 전에 먼저 가장 기본적인 형태의 인공신경망 Perceptron에 대해 알아보고자 합니다.
Perceptron?

뇌 속의 뉴런은 수많은 시냅스를 통해 다른 뉴런으로부터 전기·화학 신호를 받습니다.
각 시냅스는 얼마나 강하게 신호를 전달할지 조절할 수 있으며, 생물학적 뉴런은 경험에 따라 시냅스 강도를 키우거나 줄이며 네트워크 전체의 연결 강도를 바꿔나가며 학습합니다.

이러한 특징들을 가진 인간 뇌의 뉴런을 모델링한 초기 인공신경망이 Perceptron입니다.
뇌의 시냅스에서 강도를 조절하듯 Perceptron은 weight을 통해 값을 조정하며, 뉴런이 경험에 따라 시냅스의 강도를 키우거나 줄이듯, Perceptron 역시 오분류된 샘플에 따라 weight과 bias를 조금씩 조정해 갑니다.
$$y = \sum_{i=1}^n w_i x_i + b$$
다수의 입력값 xi에 각 입력에 대응하는 가중치 wi를 반영한 후 편향 b를 더해 최종적으로 하나의 결과 y가 출력되는 구조라고 이해할 수 있습니다.
Perceptron으로 푸는 논리게이트와 XOR
$$
y =
\begin{cases}
1, & \sum_{i=1}^n w_i x_i + b \ge 0,\\
0, & \sum_{i=1}^n w_i x_i + b < 0.
\end{cases}
$$
퍼셉트론은 위와 같이 가중합 + 임계치로 이진 출력을 만듭니다.
이 특성 덕분에, 퍼셉트론 하나를 적절한 w, b값과 함께 사용하면 논리 게이트 연산을 수행할 수 있습니다.
퍼셉트론으로 구현 가능한 AND, NAND, OR 게이트에 대해 알아보겠습니다.
AND 게이트
AND 게이트는 두 개의 입력 x1과 x2가 모두 1일 때만 1을 출력하고 그 외에는 0을 출력합니다.
이러한 AND 게이트를 퍼셉트론으로 표현하는 방식은 다음과 같습니다.
w1를 0.5, w2를 0.5로 두고 b값을 -1.5로 두게 된다면 각 입력에 대해 다음과 같은 결과를 얻게 됩니다.
| x1 | x2 | z = 1*x1 + 1*x2 - 1.5 | y |
| 0 | 0 | -1.5 | 0 |
| 0 | 1 | -0.5 | 0 |
| 1 | 0 | -0.5 | 0 |
| 1 | 1 | 0.5 | 1 |
OR 게이트
OR 게이트는 두 개의 입력 x1, x2 중 하나라도 1이라면 1을 출력합니다.
OR 게이트를 퍼셉트론으로 구현하는 방식은 아래와 같습니다.
w1=1, w2=1, b=-0.5
| x1 | x2 | z = 1*x1 + 1*x2 - 0.5 | y |
| 0 | 0 | -0.5 | 0 |
| 0 | 1 | 0.5 | 1 |
| 1 | 0 | 0.5 | 1 |
| 1 | 1 | 1.5 | 1 |
NAND 게이트
NAND 게이트는 AND 게이트와 반대의 방식으로, 입력 x1, x2가 둘 다 1이 아닌 경우에만 1을 출력합니다.
w1=-2, w2=-2, b=3
| x1 | x2 | z = -2*x1 + -2*x2 + 3 | y |
| 0 | 0 | 3 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | -1 | 0 |
퍼셉트론의 한계 XOR 게이트
XOR 게이트는 x1과 x2 중 한 개만 1일 경우에만 1을 출력하는 논리입니다.

말씀드렸다시피 퍼셉트론은 직선 하나로 0과 1을 나누는 선형 분류기입니다.
좌표 평면상 XOR 논리로 1이 출력되어야 하는 점은 (0,1), (1,0) 두 점이며, (0,0)과 (1,1)은 1을 출력해선 안됩니다.
이 영역을 하나의 직선으로 구분하는 것은 불가능하며, 이는 단일 퍼셉트론의 한계입니다.
MLP (Multi Layter Perceptron)
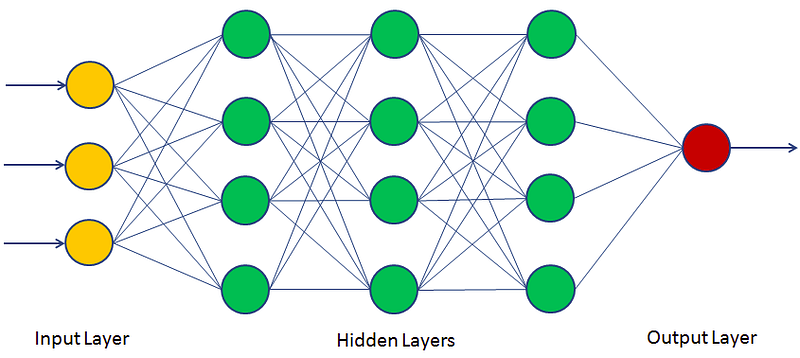
MLP는 기존 단일 퍼셉트론의 입력층과 출력층 사이에 레이어를 더한 구조입니다.
입력 -> 은닉층 -> 출력 순서로 정보가 전달됩니다.
은닉층을 추가함으로 인해 비선형 분리 문제와 같이 단일 레이어 퍼셉트론으로는 표현하지 못한 다양한 상황의 출력을 기대할 수 있습니다.
다음은 단일 퍼셉트론으로 해결하지 못했던 XOR 분류를 MLP를 이용해 해결하는 시나리오입니다.

입력 x1, x2에 대해 hidden layer의 각 노드에서 NAND 연산과 OR 연산을 수행한 후 출력층에서는 AND 연산을 수행합니다.
- (0, 0) 입력 : hidden layer의 NAND 노드의 출력이 1, OR 노드의 출력이 0이 됨으로써 output layer의 AND 연산에서 0으로 반환
- (0, 1) 입력 : hidden layer의 NAND 노드의 출력이 1, OR 노드의 출력이 1이 됨으로써 output layer의 AND 연산에서 1로 반환
- (1, 0) 입력 : hidden layer의 NAND 노드의 출력이 1, OR 노드의 출력이 1이 됨으로써 output layer의 AND 연산에서 1로 반환
- (1, 1) 입력 : hidden layer의 NAND 노드의 출력이 1, OR 노드의 출력이 1이 됨으로써 output layer의 AND 연산에서 1로 반환
# 02. Text -> Embedding
저희가 사용하는 자연어를 컴퓨터가 그대로 계산에 사용할 수는 없습니다.
따라서 텍스트를 숫자 형식의 데이터로 변경해야 하는데 이 과정을 Embedding이라고 합니다.
Transformer에서의 Embedding 과정은 총 세 단계로 이루어져 있습니다.
Tokenization
토큰화란 텍스트를 적절한 단위로 나누고 숫자 ID를 부여하는 것입니다.
이 '적절한 단위'는 자음이나 모음이 될 수도 있고, 크게는 단어 단위가 될 수도 있습니다.
토큰화를 큰 단위로 할수록 텍스트의 의미가 잘 유지됩니다.
"개쩌는 개발자 될 사람"을 단어 단위로 토큰화한다고 할 경우 "개쩌는", "개발자", "될", "사람"은 단위 토큰이 하나하나 명확하게 무엇을 의미하는지 잘 알 수 있습니다.
하지만 단어의 숫자만큼 토큰 아이디가 필요하기 때문에 사전의 크기가 커진다는 단점이 있고요.
또한 "개쩌는"과 같이 토큰화 사전에 존재하지 않을 확률이 있는 단어들에 대해서는 OOV (Out of Vocabulary) 문제가 생길 수 있습니다.
반면, 같은 문장을 자모 단위로 토큰화할 경우 OOV 문제를 해결할 수 있지만, "ㄱ", "ㅐ", "ㅉ", "ㅓ", ..... 단위 토큰 하나하나가 명확하게 무엇을 나타내는지 의미를 유지하기가 쉽지 않습니다.
이로 인해 최근에는 자주 나오는 단어는 그대로 유지하고 가끔 나오는 단어에 대해 더 작은 단위로 나눠는 방식인 subword 방식이 토큰화의 표준이 되었으며, 이로 인해 텍스트의 의미를 최대한 유지하면서도 사전의 크기는 작고 효율적으로 사용할 수 있게 되었습니다.
Token Embedding
텍스트를 토큰 ID로 바꾼 뒤, 이를 dense vector로 변환하는 단계이며, 간략하게 아래 세 단계로 나눠 볼 수 있습니다.
1. Embedding Matrix 준비
크기 $\lvert V\rvert \times d_{\mathrm{model}}$의 행렬을 하나 만듭니다.
$\lvert V\rvert$는 토큰 사전의 크기, $d_{\mathrm{model}}$은 모델이 사용하는 임베딩 차원입니다.
이 행렬의 각 행은 토큰 하나에 대응하는 학습 가능한 벡터입니다.
Positional Embedding
RNN과 트랜스포머의 가장 큰 차이점은 입력을 순차적으로 처리하는지에 있습니다.
RNN은 입력을 순차적으로 처리함에 반해 Transformer는 모든 입력을 동시에 처리하기 때문에 이 과정에서 순서 정보가 사라지게 됩니다.
하지만 텍스트에서 순서는 매우 중요한 정보이기 때문에 고려하지 않을 수가 없는데, 병렬로 처리되는 입력에 대해 순서 정보를 부여해 주는 과정이 바로 Positional Embedding입니다.
$$
\begin{aligned}
\mathrm{PE}(pos,2i) &= \sin\!\biggl(\frac{pos}{10000^{\tfrac{2i}{d_{\mathrm{model}}}}}\biggr),\\
\mathrm{PE}(pos,2i+1) &= \cos\!\biggl(\frac{pos}{10000^{\tfrac{2i}{d_{\mathrm{model}}}}}\biggr).
\end{aligned}
$$
짝수 인덱스에는 sin 함수를, 홀수 인덱스에는 cos 함수를 주기적을 배치해 서로 다른 주파수로 위치 정보를 표현하며, 결과적으로 가까운 위치끼리 비슷한 PE 벡터를 갖고, 멀리 떨어진 위치일수록 벡터 차이가 커집니다.
# 03. Attention
Attention은 트랜스포머 아키텍처의 핵심이라고 볼 수 있는 메커니즘입니다.
먼저, Attention의 사전적 의미를 살펴보겠습니다.
[불가산]
1. 주의(력), 주목
2. (보통 수식어와 함께) 돌봄, […에의] 배려[to ‥]; (기계 등의) 손질
3. 정중, 친절, 호의; (attentions) 여러 가지의 정중[친절]한 행위, (교제 중인 여성에 대한) 배려, 다정한 행동, (특히) 쓸데없는 참견
텍스트를 처리하는 관점에서 Attention의 의미를 살펴보면, 입력한 텍스트에서 관련성이 높은 단어끼리 '주의 깊게 본다'는 의미라고 이해할 수 있습니다.
Transformer에서는 이렇게 단어 사이의 관계를 계산해 관련이 있는지 찾고, 관련이 있는 단어의 맥락을 포함시켜 단어를 재해석하는 과정을 위해 Query, Key, Value의 개념이 도입되었습니다.
- Query : 검색어
- Key : Query와 관련이 있는지 계산하기 위해 문서가 가진 특징
- Value : Key의 임베딩 값
Attention의 핵심 연산을 한 줄로 표현하면 아래와 같습니다.
$$
\mathrm{Attention}(Q,\,K,\,V)
= \mathrm{softmax}\!\Bigl(\frac{Q\,K^\top}{\sqrt{d_k}}\Bigr)\,V
$$
- $Q\in\mathbb{R}^{L_q\times d_k}$는 Query의 행렬이며,
- $K\in\mathbb{R}^{L_k\times d_k}$는 Key의 행렬입니다.
차원 $d_k$가 커질수록 내적값의 분산이 커지는데,
이를 $\sqrt{d_k}$로 나누어 주면 softmax가 한쪽으로 치우치지 않고 안정적으로 동작합니다.
$$
\mathrm{softmax}(z)_i
= \frac{\exp(z_i)}{\sum_{j=1}^{K}\exp(z_j)},
\quad i=1,2,\dots,K
$$
softmax는 입력받은 값을 출력으로 0~1 사이의 값으로 모두 정규화며 출력 값들의 총합을 항상 1이 되도록 하는 함수입니다.
마지막으로 확률 분포를 $V\in\mathbb{R}^{L_k\times d_v}$에 곱해, "중요도가 높은 값"일수록 더 많이 반영된 문맥화된 출력 벡터를 생성합니다.
Self-Attention
이러한 Attention 연산을 자기 자신을 입력 대상으로 수행하는 것을 Self-Attention이라고 합니다.
X는 Token Embedding과 Positional Encoding을 더한 값으로, Transformer 블록으로 들어가는 초기 입력입니다.
보통 아래와 같이 정의합니다.
$$
X = \bigl[x_1 + \mathrm{PE}(1),\;x_2 + \mathrm{PE}(2),\;\dots\bigr]
\in\mathbb{R}^{L\times d_{\mathrm{model}}},
$$
여기서 xi는 Token Embedding, PE(i)는 Postional Encoding 벡터입니다.
이 초기 입력값을 통해 Attention 연산에 사용될 Q, K, V값을 구합니다.
$$
Q = X W^{Q},\quad
K = X W^{K},\quad
V = X W^{V}
$$
Multi-Head Attention
$$
\begin{aligned}
\mathrm{head}_i
&= \mathrm{Attention}\bigl(QW_i^Q,\;KW_i^K,\;VW_i^V\bigr),\\
\mathrm{MultiHead}(Q,K,V)
&= \mathrm{Concat}(\mathrm{head}_1,\dots,\mathrm{head}_h)\,W^O
\end{aligned}
$$
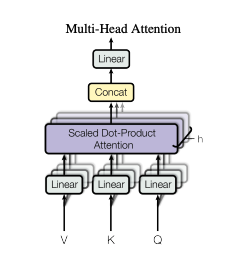
Attention Layer가 여러 개 존재해 병렬적으로 Attention을 수행하는 방법을 Multi-Head Attention이라고 합니다.
Masked Multi-Head Attention
일반적인 Multi-Head Self-Attention에 mask를 씌워 future positions (미래 토큰)이 Decoder 자기 회귀 과정에서 보이지 않도록 막아주는 기법을 Masked Multi-Head Attention이라고 하며, 지금까지 생성된 토큰만 보고 다음 토큰을 예측해야 하기 때문에 사용됩니다.
$$
\mathrm{MaskedAttention}(Q,K,V,M)
= \mathrm{softmax}\!\Bigl(\frac{Q\,K^\top}{\sqrt{d_k}} + M\Bigr)\,V,
\quad
M_{ij}=
\begin{cases}
0, & j \le i,\\
-\infty, & j > i
\end{cases}
$$
M은 look-ahead mask 행렬로, Decoder가 미래 토큰을 보지 못하게 점수 행렬에 −∞을 더해 해당 위치에 대한 Attention 가중치가 0이 되도록 만드는 역할을 합니다.
Cross-Attention
Encoder-Decoder 구조에서, Decoder가 "Encoder가 이해한 문맥"을 참조하도록 만드는 Attention을 Cross-Attention이라고 합니다.
$$
Q = X_{\mathrm{dec}}\,W^{Q},\quad
K = H_{\mathrm{enc}}\,W^{K},\quad
V = H_{\mathrm{enc}}\,W^{V}
$$
여기서 $X_{\mathrm{dec}}$는 디코더의 입력을, $H_{\mathrm{enc}}$는 인코더의 출력을 뜻합니다.
이렇게 얻은 Q, K, V를 일반 Attention과 동일한 방식으로 계산합니다.
# 04. Add & Norm 과 FNN
Add & Norm
Add & Norm은 Residual Connection (잔차 연결)과 Layer Normalization (층 정규화) 를 순차적으로 적용하는 연산을 묶어 부르는 용어입니다.
Residual Connection 단계에서는 블록 내부의 서브레이어 (Multi-Head Attention 혹은 FFN) 에 들어간 입력 x와 그 서브레이어의 출력을 더해 줍니다.
$$
y = x + \mathrm{Sublayer}(x)
$$
이렇게 함으로써 기울기 소실을 완화하여 깊은 네트워크에서도 입력 경로가 보존되게 됩니다. (Residual Connection이 기울기 흐름을 안정화시키는 이유까지 살펴보기엔 ... 조금 깊은 것 같습니다.)
또한, Residual Connection 절차를 통해 각 서브레이어는 residual(잔차) 즉, 입력과의 차이만 학습하도록 강제됩니다.
이로 인해 필요한 부분만 추가적으로 학습하면 되므로 최적화가 더 쉬워지고, 전체 학습 수렴 속도가 빨라지게 됩니다.
Layer Normalization은 입력 변수가 비슷한 범위와 분포를 가지게 하는 단계입니다.
딥러닝 모델에 데이터를 입력할 때, 입력 데이터의 분포가 서로 다르면 모델의 학습이 잘 되지 않습니다.
이를테면, 나이가 1세에서 100세까지 값을 가진다고 하고, 키를 mm단위로 해서 1500mm에서 2000mm 사이의 범위를 가진다고 할 때 모델이 키에 대해 과대평가를 할 가능성이 높아집니다.
이러한 문제를 해결하기 위해 Layer Normalization 단계를 거치는 것이라고 볼 수 있습니다.
$$
\begin{aligned}
\mu &= \frac{1}{d}\sum_{i=1}^d x_i,\\
\sigma^2 &= \frac{1}{d}\sum_{i=1}^d (x_i - \mu)^2,\\
\mathrm{LayerNorm}(x)_i &= \gamma_i\,\frac{x_i - \mu}{\sqrt{\sigma^2 + \epsilon}} + \beta_i,
\end{aligned}
$$
이때 $\gamma, \beta \in \mathbb{R}^d$는 학습 가능한 scale 및 shift 파라미터이고,
$\epsilon$은 분모 0 방지를 위한 작은 상수입니다.
FNN (Feed Forward Network)
앞서 MLP가 여러 층의 Perceptron을 쌓아 비선형 표현력을 높인 구조라고 했습니다.
Transformer에서는 이 MLP를 각 토큰에 독립적으로, 병렬로 적용하는 것이 FFN입니다.
Multi-Head Attention이 단어 사이의 관계를 파악하는 역할이라면, FNN은 입력 텍스트 전체를 이해하는 역할이라고 볼 수 있습니다.
FNN의 구성은 다음과 같습니다.
- Linear Layer : 실질적인 학습이 이루어지는 계층
- Dropout Layer : Overfitting을 방지하기 위해 각 Linear Layer 이후에 확률적으로 뉴런을 비활성화
- Layer Normalization : 입력 변수가 비슷한 범위와 분포를 가지게 하는 단계
- Activation Function : 비선형성 부여
$$
\mathrm{FFN}(x)
= \mathrm{ReLU}(xW_1 + b_1)\,W_2 + b_2,
$$
ReLU는 Activation Function의 한 종류입니다.
# 05. Encoder & Decoder
앞서 살펴본 Transformer의 구성 요소들을 조합하여 모델을 Encoder와 Decoder를 구성합니다.
Encoder
Encoder는 입력 문장을 문맥화된 벡터 시퀀스로 변환하는 역할을 합니다.
다음 순서로 구성됩니다.
- Multi-Head Attention
- Add & Norm
- FFN
- Add & Norm
Decoder
Decoder는 생성을 담당하는 부분으로, 지금까지 생성된 토큰을 입력으로 받아 Encoder 출력에서 문맥 정보를 참조하고 최종적으로 다음 토큰의 확률을 계산해 내는 구조입니다.
다음 순서로 구성됩니다.
- Masked Multi-Head Attention
- Add & Norm
- Multi-Head Attention
- Add & Norm
- FFN
- Add & Norm
토큰화부터 디코더까지 트랜스포머 한바퀴를 돌아봤습니다.
생각보다 내용이 많네요.
사실 하루면 글을 다 작성하겠다 싶었는데, 해당 과목 시험 본 후에서야 포스트를 완성하게 되었답니다.